≫つぎへ　　　≫　もどる　　　　≫　メニュー　　≫　つぎへω

６　に ついて
  

koujichuu211118



※ この ファイル は　６ ÷ ０　に おいて わられる 数 【 ６ 】 と 差 を　なくすこと についてかんがえてみる


。。。。一般角 360°＝:　一般角 0°

。。。。。 。(-1)²　＝:　(-1)⁰

。。..。パイラジアン＝:　180°

。..。2 パイラジアン＝:　0 パイラジアン

。。。。。。。ｉ⁴　＝:　ｉ⁰
     

>　　シクスタンス （六分儀；ロクブンギ）＝ 60°の カクド単位
1シクスタンス　＝　 60°
6シクスタンス　＝　360°
6 シクスタンス　＝：　0 シクスタンス
　>　シクスタンス （六分儀；ロクブンギ）＝ 60°の カクド単位
　>　1シクスタンス　＝　 60°
　>　6シクスタンス　＝　360°




イ　チ ムゲン すべて

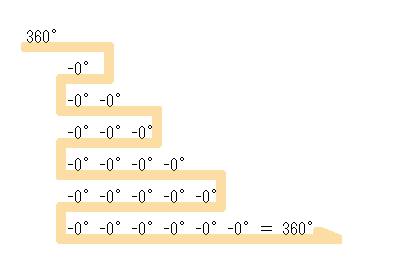
算数 版　
ルイゲン 式　		 ．
．
．
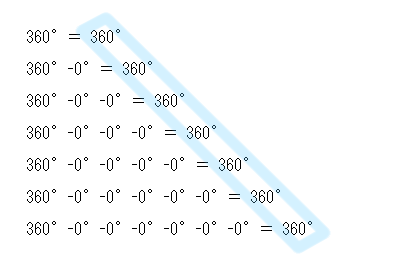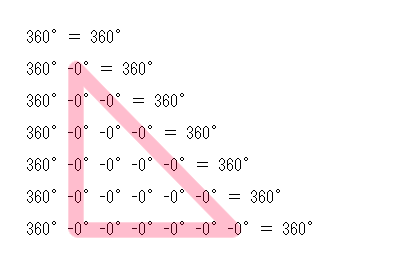【 きざむ 】 とは… 座標 ヶ所 数 理論限界回数 一致可能回数 ．
．
．
【 ピッタリ 】とは… ■ 【 なん ヶ所 】に きざめるのか ■ なん回め 【 まで 】 ひけるのか ■ なん回め で 一致 する 【 可能性 】 があるか ．
．
．
結　果　 360°地点 のみ なん回でもひけてしまう なん回めで くぎっても 一致 してしまう ．
．
．
結　論　 １ヶ所 きざめる ∞回 演算可能 なん回め でも 成立 ．
．
．
1 setsu check

ゼ　ロ ± ﾑｹﾞﾝ な　し ．
．
．
算数 版　

ルイゲン 式　		 ．
．
．
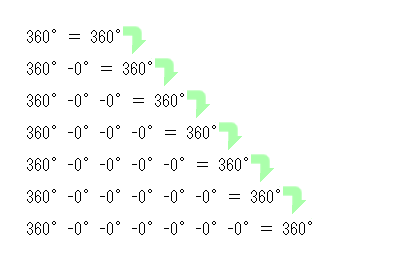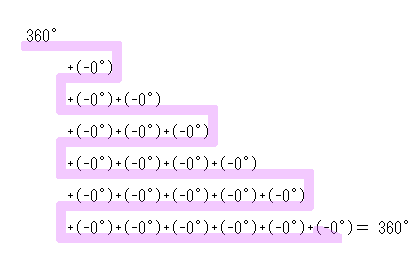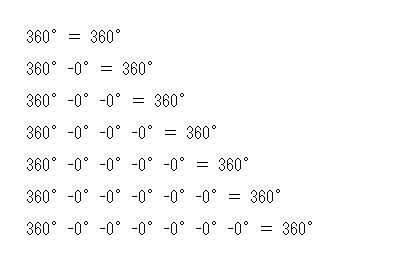【 きざむ 】 とは… 歩数所変位回数 左右回転 理論限界値 累計回転量到達回数 ．
．
．
【 ピッタリ 】とは… ■ 座標 が 【 うごいた 】 回数 ■ なん回 め 【 まで 】 反数 を たせるのか □ 位置 でなく 【 量 】 が 一致 しなければならない
最終的に ＝ 0°が 右はしにきてもらわないといけない		 ．
．
．
結　果　 360°地点 から 1 回 も うごいてない なん回でも たしひきひできてしまう なん回実行しても 量 としての目標 は達成できない ．
．
．
結　論　 0 回 うごいた ±∞ 回 演算可能 な　し ．
．
．
なし　目標回転運動量達成回数





どのタイミングで 『 キザんだ 』 と カウント するか

何回キザんだかは 『 』 をみればわかる…

キザんだ回数 は 『 』 に あらわれることを 信じる…



 

トランプをやっていて

『 え…？』
『 いま…、オレの 番？』 と きいたことはないだろうか？

あのシュンカン、あたまのなかで ゼロ除算 が おきているかもしれない…

条件：
わられる数 が 循環していること。
わられる数 が 最大値。で 最終値。

その条件がそろっていれば
任意の数。任意の単位。でつかえる

ゴンドラ 30個 　　
公園一周並木48本　
トランプ 6人　　　
時計の時間　 　		 　30 番目
　48 本目
　 6 番目
　 24 時　

…など 順序 さえきめれば いくらでもつかえる可能性はふやせる

計算は いったん カクドに単位をおきかえてするが、
円型でなくても
回転するものでなくても 【 一周 していれば 】 計算はできる


カクド単位 なら 式をつくれるが…　度° や ラジアン や シクスタンス など…(位置方向)

回転数単位 では 式をつくれない…　rpm　rot　trun など…(回転量)

単位はどれでもいいが
360°が 約数 がおおいから
わられる数 はいったん → 360°という 値におきかえる




式 の ていあん


算数版の式　　　　　　　　360°の ルイゲン

　6 ÷ 2 ＝ X　なら

　① わられる数（任意の数：例 6 ） を いったん 360 にする。。
　② カクド単位の 【 °（ど）】をつける
　③ わる数 を 比率倍 する
　④ カクド単位の 【 °（ど）】をつける


6 を 60 倍 したから
2 も 60 倍 する

　360°÷　120°＝ この方法で 3 がもとまる

　6 ÷ 2 ＝ 3



が、（この形式ではゼロ除算におうじられないので）


　360°÷　120°⇒

これを ルイゲン で あらわす

　360°-120°-120°-120°＝　0°

　　　　　-120°を【 3回 】おこなったから

　　　　　 360°÷　120°＝　3

もし
　123.4 ÷ 30.85 なら　⇒

　わられる数 を 360°に するために

　わる数 と わられる数を 2.917倍する

　　　　　 360°÷　90°＝　X

　360°-90°-90°-90°-90°＝ 0°

　　　　　-90°を【 4回 】おこなったから X ＝ 4



　算　数　版 の 式

この方法 を ゼロ除算につかってみる

　6 ÷ 0 　⇒

360°-0°（-0°-0°-0°…）＝ 360°
　　　　　　　　　　　　＝ 0°

あとは 【 回数 】の カウント方法 ( 上の表 ) の
主張する 【 説 】 によって その 答 がかわる


。。。。 数学版の式　　　　　　　　　　　マイナス１の しすうルイゲン

　6 ÷ 2 ＝ X　なら

　① わられる数（任意の数：例 6）を いったん しすう 2 にする
　② （-1）2 の ように （-1） のしすう にもってくる　　
　③ わる数 を 比率倍する
　④ それを（-1）の しすう 2 を わるかず にする。。


6 を 0.333 倍 したから
2 も 0.333 倍 する

　（-1）（2÷0.666）＝ この方法で (-1) 3 が もとまる　
　　　　　　　　　　　　　　　（ しすう が ワリザンの答 X になる）。
　6 ÷ 2 ＝ 3　


が、（この形式ではゼロ除算におうじられないので）

　（-1）（2÷0.666）　⇒

これを ルイゲン で あらわす

　（-1）（2-0.666-0.666-0.666）　＝　（-1）⁰

　　　　　-0.666　を【 3回 】おこなったから　

　　　　（-1）2÷0.666 ＝（-1）3

もし
　123.4 ÷ 30.85 なら　⇒

　わられる数 を （-1）2 に するために

　わる数 と わられる数を 0.0162倍する

　　　　（-1）2÷0.5 ＝（-1）X

（-1）（2-0.5-0.5-0.5-0.5）＝　（-1）⁰

　　　　　-0.5　を【 4回 】おこなったから X＝ 4



　数　学　版 の 式

この方法 を ゼロ除算につかってみる

　6 ÷ 0 　⇒

（-1）（2 -0 （-0 -0 -0…））＝（-1）²
　　　　　　　　　　　 　＝（-1）⁰

あとは【 回数 】の カウント方法 ( 上の表 ) の
主張する 【 説 】 によって その 答 がかわる





ueki zan