≫　もどる　　≫　マップ　　　≫　あーぎゅめんと　　　　≫　しす カケザン　　　≫　..ビジョン　　　≫　２アイ２　　　　..≫　100　　　≫　４ じょう　　

231105　　　　　ラジアン


きょり km　×　0.009


　　　　

	l1l\sr\0-k3\kyo\cos\a-kk-3-r.html　　　せんかいず -\l1l\sr\0-k3\kyo\cos\a-kk-3.html まず　パイ　 で→　パイラジアン で→　ラジアン　　　　　←　がっこうとは　ぎゃくじゅん 適当な数字をいってもらう ど→ラジアン ど→パイ　　　を　やる rad argument ラジアン　が　でてきたのは　ω　の確認　 　2ω　3ω　4ω　の図 　リンク 　-2.094..ラジアン　が　なぜ　240ど　に　なるのか 簡易的な説明で　57.3ど　くらい　－2.094　くらい を … 　　　　　　　　　60ど　くらい　－2　くらい と …イメージしてもらい 　－120　ど　は　プラスかいてんでいうところの　240　ど　だと かみくだいていった … 　えいえん　に　ケタ　が　つづくんだったら 　なぜ　240ど　に　【∠ぴったり】なるといいきれるのか？ 　について … 　　説明する 　みじかな数　たとえば　２　でわった　あと　２　でかけると　どうなるかについて 　もとにもどる 　ex. 　７　÷　２　×２　＝　７ おなじく 　１７　でわった　あと　１７　でかけると　どうなるかについて　 ex. ７　÷　１７　×　１７　＝　７ 　やはり　もとにもどります 　それは　×カケザン　と　÷ワリザン　が　ぎゃくえんざん　の　 　 　かんけいに　あるからになります 　これは　もちろん　しょうすう　に　しても　おなじことが　おこります 　ぎゃくえんざん　だからに　なります 　ex. ７７　÷　1.2　×　1.2　＝　７７ 　ここから、わったかず　と　おなじかず　で　かけると　もとにもどる　ことがわかります 　ここで　えんしゅうりつ　( 3.14.. )　に　ちかい　３　で　やると 　どうなるか　みていきます 　 　ex. ７７　÷　３　×　３　＝　７７ 　もとに　もどっています 　さらに　ちかい　3.1　だと　どうなるか　というと 　ex. ７７　÷　3.1　×　3.1　＝　７７ 　やはり　もとに　もどってきます では　がっこう　であつかう　きんじち　3.14　では　こうなります 　ex. ７７　÷　3.14　×　3.14　＝　７７ 　やはり　もとに　もどってきます では、 　これが　まぎれも　ない　ほんものの　えんしゅうりつ　兀　だと　どうなるでしょう 　これを　てけいさん　の　ひっさん　で　かくにんすることは　ムゲンのじかんが　かかります 　 　なぜなら　兀　は　3.14..のあとに　ムゲンけた　つづいていくからです 　しかし、これが　ぴったりに　もどることは　すぐに　かくにんできます 　ex. ７７　÷　兀　×　兀　＝　７７ 　windows の　デンタクにも　兀　ボタン　が　あります 　７７　÷　の　あとに　兀　ボタン　を　おして 　その　あとで　×　兀　ボタン　を　すれば　 　わられる　かず　が　どんな　かず　(７７ いがい)　でも　 　もとに　もどってくることが　かくにん　できます
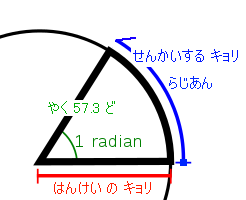
	￣￣￣￣￣￣ 　ラジアン　　と　　パイ　 ￣￣￣￣￣￣ 　　ラジアン　の　およそ　５７.３　ど　というもの　の　しょうたいは　 　　１８０ど　÷　えんしゅうりつ 兀　 　　に　なっています 　　１８０　÷　３.１４.. 　　で 　　＝　∠５７.２９５７７９５１３ …　ど 　　となります 　　そして　これと　ほぼ　まったく　おなじ　タイミング　で　登場するのが 　　「　カクド　たんい　として　の　∠ パイ　」 　　に　なります 　　なぜ　どうじ　に　おそわるかというと　 　　セット　で　おぼえたほうが　おたがいの　とくちょうを　リカイ　しやすいから 　　になります 　　３.１４.. ラジアン　＝　１８０　ど　 　　これを　　　　　　 ＝　１　パイ　 　　と　よびます.. 　　１パイ　は　１パイラジアン　と　まったく　おなじになります 　　ここが　ようちゅうい　に　なります 　　１パイ　＝　１パイラジアン　　＝　３.１４..ラジアン　＝　１８０ど　＝　はんしゅう 　　もういちど　かいて 　　１パイ　は　１パイラジアン　と　まったく　おなじになります 　　ここが　ようちゅうい　に　なります 　　　０.１パイ　＝　１８ど 　　０.０１パイ　＝　１.８ど 　　になります　　 　　がっこうでは　↓ここまで　おおきい カクド　は　でてきませんが 　　∠３１４　ラジアン　＝　∠１００　パイ　 　　りくつ　としては　(ほぼ)　こうなります 　　∠３１４　ラジアン　＝　∠１００　パイ　　＝　(５０しゅうして)　０ど 　　はんしゅう　が　１００回　おこなわれるので　↑こうなります
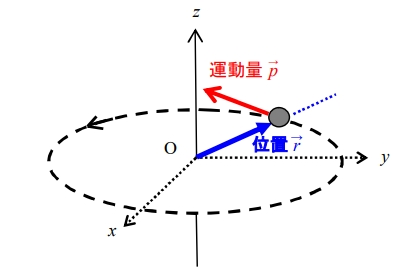
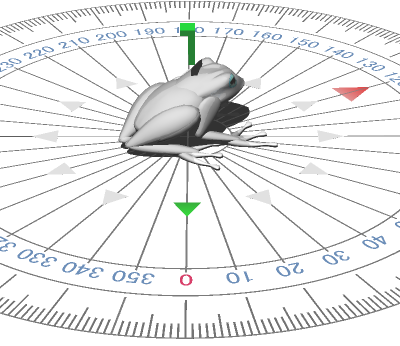
	￣￣￣￣￣￣ 　オメガ　　は　　３　ぶんの　２　パイ　 ￣￣￣￣￣￣ へんかく　しーた　θ　に　こうかかれています 　３　ぶんの　２　パイ　 　これが　１２０ど　で　あることを　かくにん　します 　１パイ　　　　　 ＝　１８０ど 　３ ぶんの１パイ　＝　　６０ど 　３ ぶんの２パイ　＝　１２０ど となります 　ラジアン　たんい　でみると …　なにやら　とっつきづらそうな　 　かくど　に　みえますが 　2.094..ラジアン これ　の　なりたち　から　さかのぼっていくと 　120　ど 　に　なることが　みえてきます 　2.094..　というのは 　　2.094..　(ラジアン) 　　＝　120　ど　？ 　　2.094..　×　(180 ど　÷　3.14..)　 ＝　120　ど　？ 　 ( 3.14..× 2 ÷ 3 )　×　(180　÷　3.14..)　 ＝　120　ど　？　 　 ( 3.14..　÷　3.14..) ×　2　÷　3　×　180 ＝　120　ど　　 ？　 　　 　　1　×　2　÷　3　×　180 ＝　120　ど　　？ 　　180　÷　3　×　2　＝　　120　ど　　　 …　○ ここから　きています 　　ぜんはん　に　×　パイ　と 　　こうはん　に　÷　パイ　が 　　あるから　ぴったり　きれいに　うちけせます　 これで　ムゲンけた　かくにん　しなくても　 　ぴったり　１２０ど　に　なることが　わかります デンタク　の　パイボタン　を　つかってかくにんができます ラジアン　＝　180　÷　えんしゅうりつ