ためし kei-san ω
□|-1| □|i| □1^2 □2^0 □i+i □arg -i □45.30deg □ abs i →ω ≫
i4ω3
.jpg)
.jpg)
≫
チズ

.jpg)
ためし kei-san ω
□|-1| □|i| □1^2 □2^0 □i+i □arg -i □45.30deg □ abs i →ω ≫
i4ω3
.jpg)

.jpg)
≫
チズ


.jpg)
カケザン左回転 ワリザン右回転 360deg 1 × 1 1 × 1 × 1 1 × 1 × 1 × 1 1 ÷ 1 1 ÷ 1 ÷ 1 1 ÷ 1 ÷ 1 ÷ 1 カケザン左回転 ワリザン右回転 180deg - 1 × - 1 - 1 × - 1 × - 1 - 1 × - 1 × - 1 × - 1 - 1 ÷ - 1 - 1 ÷ - 1 ÷ - 1 - 1 ÷ - 1 ÷ - 1 ÷ - 1 カケザン左回転 ワリザン右回転 90deg i × i i × i × i i × i × i × i i ÷ i i ÷ i ÷ i i ÷ i ÷ i ÷ i i ÷ i ÷ i ÷ i ÷ i 1 × - 1 1 × i 1 × - i 1 1 1 2 1 3 1 4 1 100 |
 .jpg) .jpg) .jpg) |
 . . |
arg ( 3 + 3 i ) arg ( 1 ) arg ( -1 ) arg ( i ) arg ( -i ) |
= 45° = 0° = 180° = 90° = -90° |
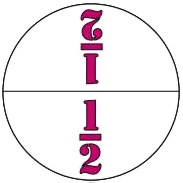 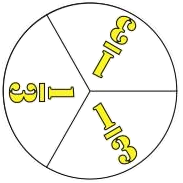 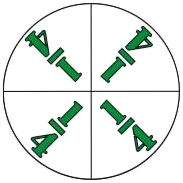 |
1 0.5 1 0.333 1 0.25 |
2 回かけると 1になるかず -1 …180° 3 回かけると 1になるかず ω ω …120° 4 回かけると 1になるかず i -i -1 …90° |
______.jpg) クリック ___ |
25 + 75 5 2 + 8.66 2 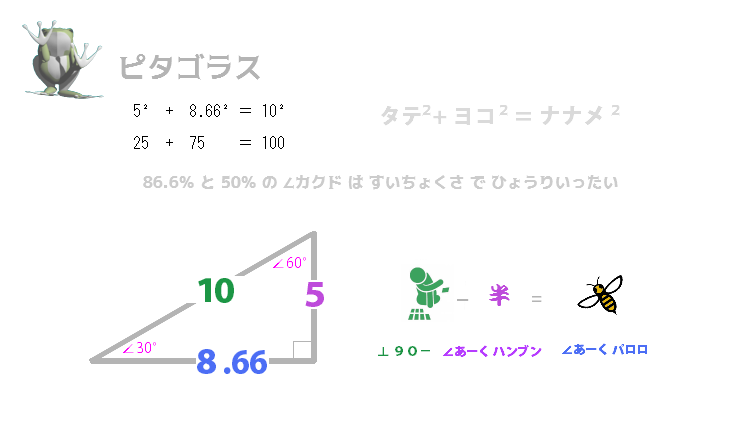 四捨五入 白金比 オメガ √3 5 8.66 斜辺 50 86.6 斜辺 0.5 0.866 斜辺 5 × 1.732 -- ω性質 なぜそうなるのか?が きになるばあい、のみ、 … これ↓。 すこしフクザツ。 ω 3じょうこん オメガ 式χ3=1 3乗 因数分解 解 の 公 式 公式 導 出 wolf ↑ きにならないばあいは、つぎへ↓とばす… 『 どうやら、そういうかず になるらしい 』ってこと。で、なっとく の いく ひと は ↓つぎ へ とばす…(わるぎなく) ω × ω × ω ------ ω 3 ---- 100 × ω ----- 2 × ω --- 3 × ω --- ω × ω --- ω 2 --- ↑↓ オメガ 2 は オメガーバー ω --- ω × ω 2 --- ω × ω × ω × ω --- ω 4 --- ω - ω --- ω + ω --- ω + 2ω --- 2ω + 8ω --- ω + ω --- ω + ω --- ω 2 + ω --- 2ω + 2ω --- 2 × ω × ω × ω --- 2ω 3 --- 2ω × ω --- 2ω × ω × ω --- cis120deg --- cis0deg --- cis240deg --- cis360deg --- 30deg^2 --- |
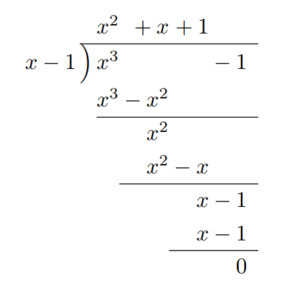
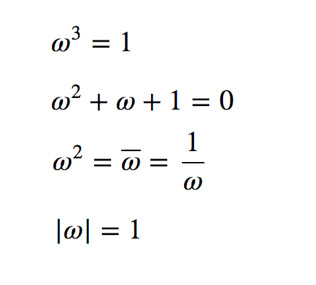
| カケザン左回転 ワリザン右回転 45deg arg ( 3 + 3i ) = 45° 30 deg arg ( 173.2 + 100i ) = yaku 30° arg ( √3 + i ) = 30°just arg ( (√3) * 100 + 100i ) = 30°just arg ( 866 + 50i ) = 30.0007° arg ( 0.866 + 0.5i ) = 30.0007° みやすく へんしゅう 四捨五入 版 ↑0.0007°などの ごさ を すっきりみせる arg(0.5i+0.866) https://ja.wolframalpha.com/input?i=round%28degrees%28arg%280.5i%2B0.866%29%29%2C0.01%29 arg((0.5i+0.866)^2) https://ja.wolframalpha.com/input?i=round%28degrees%28arg%28%280.5i%2B0.866%29%5E2%29%29%2C0.1%29 arg((0.5i+0.866)^3) https://ja.wolframalpha.com/input?i=round%28degrees%28arg%28%280.5i%2B0.866%29%5E3%29%29%2C0.1%29 arg((0.5i+0.866)^4) https://ja.wolframalpha.com/input?i=round%28degrees%28arg%28%280.5i%2B0.866%29%5E4%29%29%2C0.1%29 arg((0.5i+0.866)^5) arg((0.5i+0.866)^6) arg((0.5i+0.866)^7) arg((0.5i+0.866)^8) arg((0.5i+0.866)^9) https://ja.wolframalpha.com/input?i=round%28degrees%28arg%28%280.5i%2B0.866%29%5E9%29%29%2C0.1%29 arg((0.5i+0.866)^10) https://ja.wolframalpha.com/input?i=round%28degrees%28arg%28%280.5i%2B0.866%29%5E10%29%29%2C0.1%29 arg((0.5i+0.866)^11) arg((0.5i+0.866)^12) https://ja.wolframalpha.com/input?i=round%28degrees%28arg%28%280.5i%2B0.866%29%5E12%29%29%2C0.1%29 arg((0.5i+0.866)^0) https://ja.wolframalpha.com/input?i=round%28degrees%28arg%28%280.5i%2B0.866%29%5E0%29%29%2C0.1%29 arg((0.5i+0.866)^1) arg((0.5i+0.866)^-1) https://ja.wolframalpha.com/input?i=round%28degrees%28arg%28%280.5i%2B0.866%29%5E-1%29%29%2C0.1%29 arg((0.5i+0.866)^-2) arg((0.5i+0.866)^-3) https://ja.wolframalpha.com/input?i=round%28degrees%28arg%28%280.5i%2B0.866%29%5E-3%29%29%2C0.1%29 じっさいに入力しているしき↓ round(degrees(arg((0.5i+0.866)^5)),0.1) ししゃごにゅう(ぶんどき単位(カクド(ふくそすう)^なんじょうしたか),ししゃごにゅうするケタのくらい) |
||
| ___ |
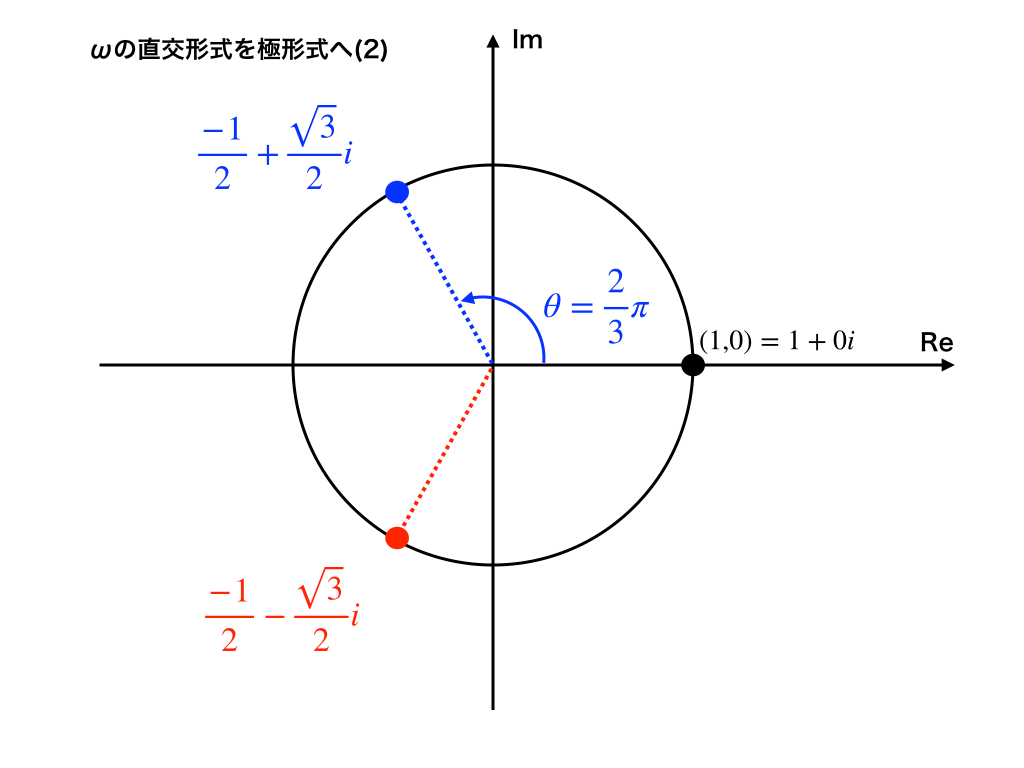
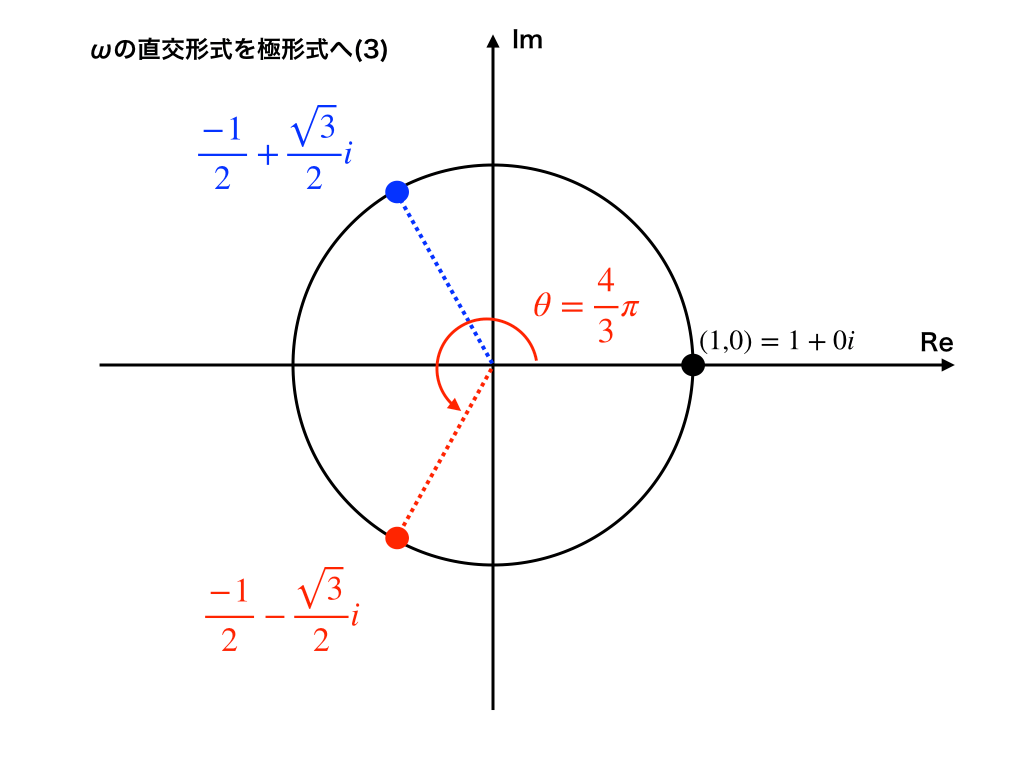
3 じょうこん オメガ と オメガーバー オメガ 120°回転 arg (ω) ≫ オメガ を かけると 左 まわり で 120°回転 オメガ で わると 右 まわり で 120°回転 ((-1 + sqrt3*i)/2) =: ω オメガ 120°回転 オメガ を しょうすう で かくと ほぼ この あたいになる (√むりすうなので むげんにつづく) ω = - 0.5 + 0.866.. i ≫ カクニン オメガ を 2 回 かけると オメガーバー に なる ω × ω = ω ≫ オメガ の じじょう は オメーガーバー ω 2 = ω ≫ オメガーバー を 2 回 かけると オメガ に なる ω × ω = ω ≫ カクニン オメガバー の じじょう は オメガ ω 2 = ω ≫ オメガ を 3 回 かけると = 1 に なる ω×ω×ω = 1 ≫ カクニン オメガ の 3 じょう は = 1 に なる ω 3 = 1 ≫ オメガーバー を 3 回 かけると = 1 に なる ω×ω×ω = 1 ≫ カクニン オメガーバー の 3 じょう は = 1 に なる ω 3 = 1 ≫ --かけざんをさきにいれる ω 1 ÷ ω = ω arg ( 1 ÷ ω) ≫ -120o omega bar ((-1 + sqrt3*i)/2) =: ω オメガ 120°回転 ((sqrt3 + i)/2) =: ω ハニーオメガ オメガほど回転力をもっていない 30°回転 |
 |
 |