1i-omegaる
 ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ≫ もどる ≫ メニュー ≫ しょすう 乗 ≫ きょすう
( 1 いがいで …)
3じょうすると 1 になるかず …
1×1×1=1
さんかくじょうぎ に あらわれるひりつ:
はんぶん と パロロ について …
きょすう: オメガ (じゅんせい) について … →
└ふくそすう m(_ _)m
ハニーオメガ について …
ハニーオメガ の けいさんほうほう …
ハニーオメガ の ( …) …
→ ≫もどる ≫メニュー ≫ハニーオメガ
メモぺーじ
※このページは 算数っぽく かいています
【よい】=:プラス1 = 100%
オメガ と パロロ
( えがかれている せいざ は はなしの ないようと まったくかんけいありません …)
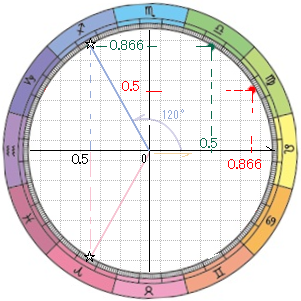
| オメガ とは …( カンイテキ な せつめい …) | |
| 。。。 | ( 1 いがいで …) 3じょうすると 1 になるかず … 1×1×1=1 ω×ω×ω=1 マイナス 1 …というすうじ を プラス 1 … が 180° かいてんした ばしょに くる すうじ だと たとえてみます … すると … オメガ は プラス 1 が 120° かいてんした ばしょに くる すうじ と たとえられます … (ほんしつてきにいうと …240°の かのうせい も さいしょは ねむっている) マイナス 0.5 と … やく 0.866 アイ という かず … ふくそすう と よばれる 2しゅるいのかず が まざった かず の きごう ω の なまえ で 3じょう すると Y字 のように 3かいてんして プラス 1 に もどってきます… このページでは この 2つ の くみあわせが じょうげさゆう ぎゃくてん で へいめんじょうで 8かしょ で この タテヨコひりつ が おこることから パロロ と ハンブン… というゴロで カンイてきに おぼえて ください… |
ぜったいち10cm
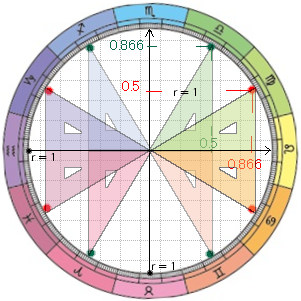
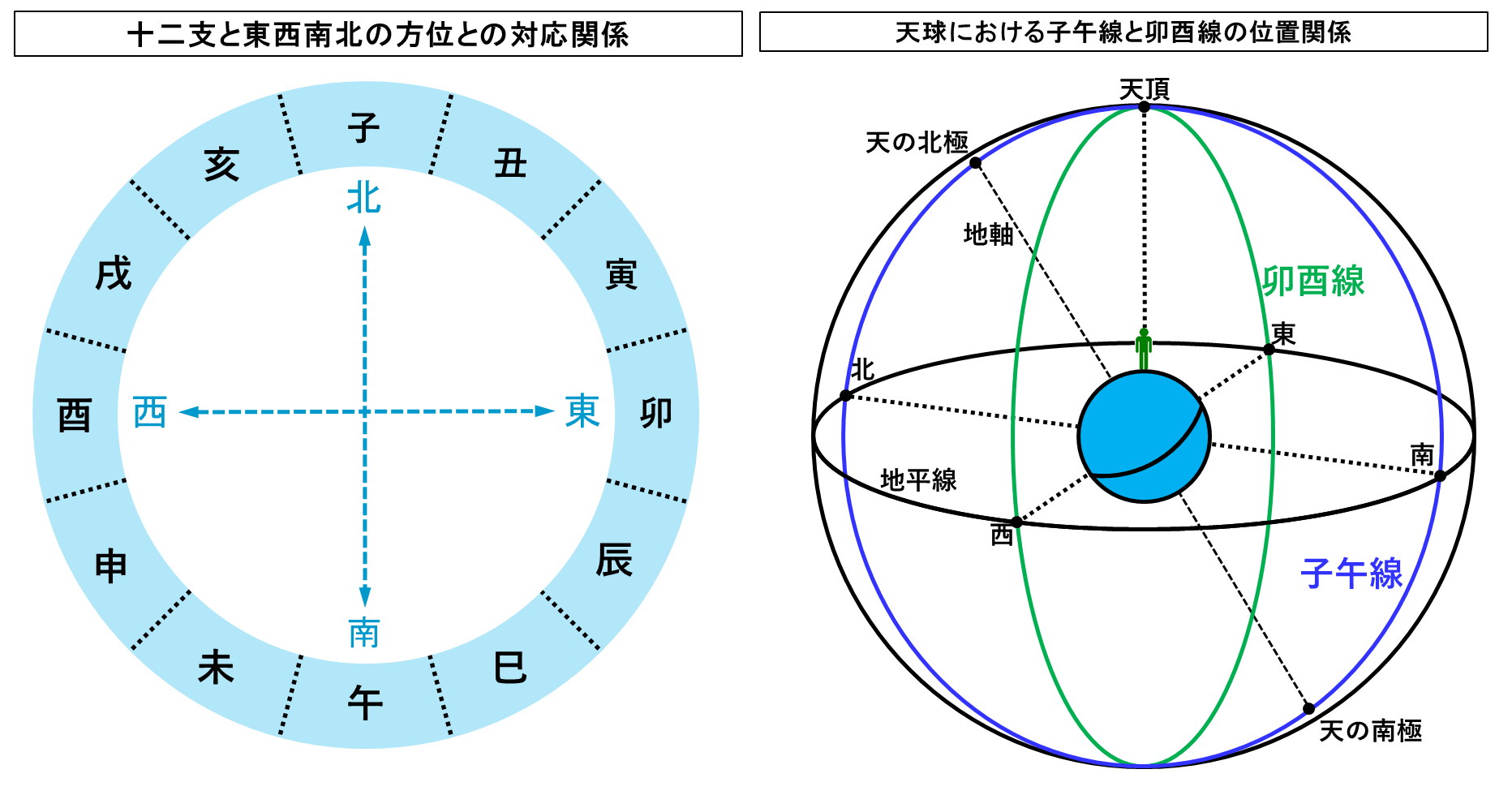
12 せいざ これら は 【 ∠ 30 ど 】 おきに ならべられています
( かりに ) あなたは きいろ ( みぎ→ ■) ほうこうに
.jpg)
すすみたい と かんがえているもの とします …
そちらに 10cm すすむことを プラス10cm ※すすんだ※ …
という ふうに いうことにします …
そして ひだり ■ ←に 10cm すすむこと を
マイナス 10cm ※ すすんだ ※ と いえる ように …
すすむ という ことば を かくちょう してみます …
ないよう とちゅう …カクカクシカジカ
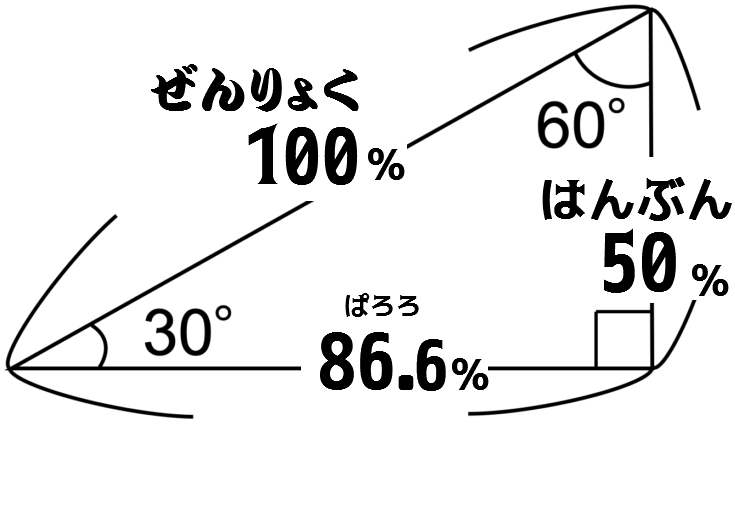
ハンブン と パロロ とは … ハンブン パロロ 50% と 86.6% ※ この すうじ ( ひりつ ) を おぼえてください … これで かなり オメガ ω という ヤツ の イメージ を つかんだ ことになります … |
さんかくじょうぎ の ながさ ひ 。 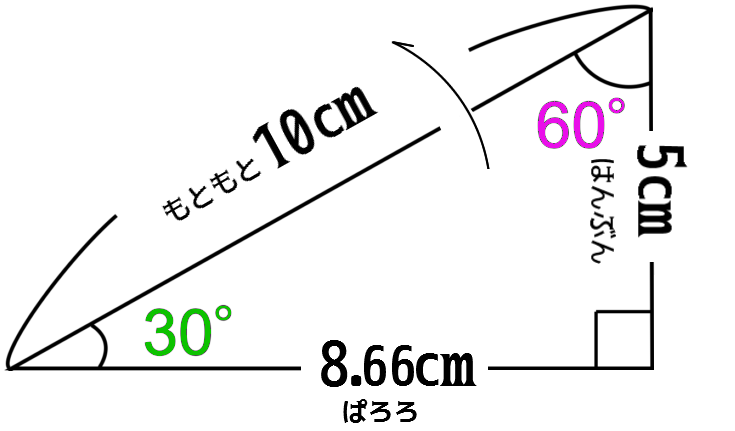 |
ハンブン 50% とは … ぜんかい ( 100 % ) の 『 はんぶん 』 の りょう のこと。 2 ぶんの 1 の こと …。 0.5 の こと … 。 (コサイン) 60°の こと … 60°の ほうこう おんち だったとしても マエ→ にすすんでいる わりあい。 ポイント は … …1こ となりが 13% へった ( 86.6% ) だったから … 2こ となりなら 26% くらいへるのでは … ? (73.2% くらい?) …とはならずに … 50% ( はんぶん ) となります … (※※ さんかく かんすうてきに へっていきます ※※) パロロ 86.6% とは … やく 87 % に なります … (コサイン) 30°の こと … 30°の ほうこう おんち だったとしても マエ→ にすすんでいる わりあい。 ぜんりょく から やく 13% へった りょう に なります 0.8660254 … … という むげんにつづく かず ( むりすう ) で いくつか よびだしかたが あります …→ が とにかく 『 パロロ 』 と おぼえれば それが 99.997% の ゴロ クオリティ になります ≫ このなかに パロロ と ハンブン が かくれています ←… |
  えっくす→ の プラスほうこう に すすむ よていだったが … 60°ズレてた … でも …はんぶん は マエ→に すすんでいる … |
 |
 ぶれ ∠30°なら … やく 87% ぶれ ∠60°なら … 50% 。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。 |
せんざいのうりょく とは? … こちら ≫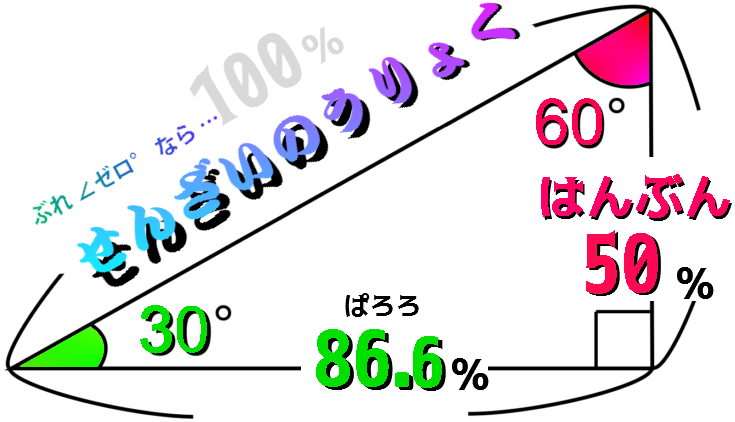 |
| じぶん の へや に ある とけい を はかってみたら たまたま 20 センチサイズ だった …  ここにも パロロ と ハンブン が あらわれます …  |
つまり さんかく かんすう … ってことに なるわけですが … いまいち、 この よびな の ひびき が ムキシツ に きこえて … ピン と こないので … かってに カ ク カ ツ リ ツ 【 角 活 率 】 と … よんでみることにします … つまり 【 ∠ カクド 】 によって 活かされる リツ !! … です … ゆうこうに なる パーセンテージ です … はたらいてくる ヒリツ です … ぎゃくに いうと … カクド に よって それて しまう リツ … でも …あります … ←じかん では なく、いちかんけい を みて … とにかく みぎ。 みぎ の 方向 に すすみたい。 みぎ に いきさえすれば けいろ は きにしない … という いしき が あったとしたとき … 3時 の ほうこう に すすめたら ベスト なんだけど … ( きがついたら 4時 のほうこう に すすんでいた… ) でも … けっかてきには … 87% くらい は ムダ じゃなかった… ということが わかる … |
0.86602540378443864676372317 …えいえんにつづく …
≫ もどる
99.997 パーセント 以上 の クオリティ を のぞむヒトが
カクニンしたくなったとき の カクニンほうほう であり …
むりやり おぼえる ことは ないです …
おぼえるとしても ① ② ③ どれかいっこ おぼえれば じゅうぶんです …
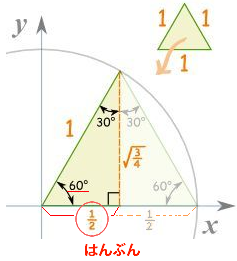
①ピタゴラス の 1 : 2 : √ルート 3 の はんぶん サイズ
√ルート 3 ひとなみにおごれやおなご
1.7320508075の はんぶん です (→カクニン)
いいかえると↑→ 50% の 辺 の ながさ を ひとなみにおごれ 1.73 倍 すると パロロになります
でんたく 3 → √ルート → ÷ → 2
②
じじょうすると …75パーセント に なるかずです
でんたく 0.75 → √ルート (→カクニン)
75% → √ルート (→カクニン)
3÷4 → √ルート (→カクニン)
√ルート の ぶぶん↑ を 0.5 じょう ^ に しても でてきます
0.75 → ^0.5 (→カクニン)
③
サイン60度。
コサイン30度。
かんすうでんたく 60 → S I N (→カクニン)
かんすうでんたく 30 → COS (→カクニン)
≫ もどる
(※ オメガ とは ちょくせつ かんけいありませんが … )
→ 【 パロロ 】 に にた 【 ナロロ 】 という ゴロ が あることに ついて きょうみ の ある方 は → こちら (+【クロロ】 …15ども ついかよてい)
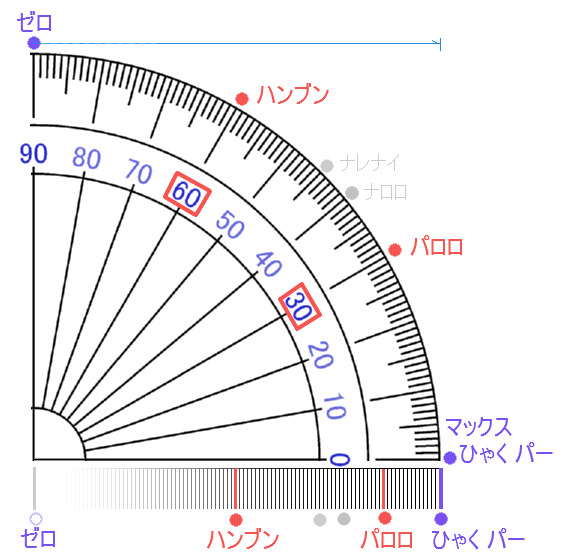
≫ それいがいの∠カクド と 活かされるわりあい について …10どきざみ ・10%きざみ ←
---------------------------------------------
つぎの ページ では 【 ※ 12 じょうこん 】
あとは それが 【 よこはば 】 に なるのか 【 たてはば 】 になるのか …
よこ なら 右 → なのか ← 左 なのか
たて なら 上 ↑ なのか ↓ 下 なのか で
8 とおり に わかれます …
よこ のうち 右 → なら プラス
よこ なら ← 左 なら マイナス
たて のうち 上 ↑ なら プラス
たて なら 下 ↓ なら マイナス で カウントすることにしてみます…
| 。。。。。。 | よこ+0.5 たて+0.866 よこ+0.5 たて-0.866 よこ-0.5 たて+0.866 よこ-0.5 たて-0.866 たて+0.5 よこ+0.866 たて+0.5 よこ-0.866 たて-0.5 よこ+0.866 たて-0.5 よこ-0.866 |
↑→→ → ↓ ↓ ← ↑ ↑ ← ↓ ↓ ↑→→ → ↓ ↓ ↓→→ ↓←← |
---------------------------------------------
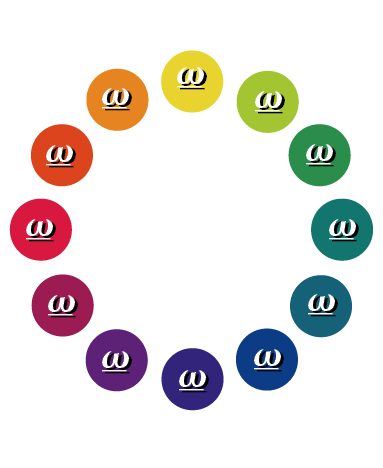
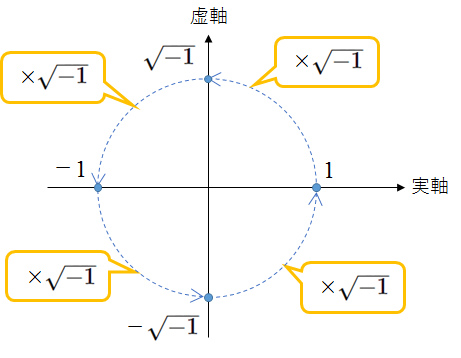
0.5ⅰ + 0.866
( 30度 かいてん の 1。 ) の こと を
かりに
ω
と かくことにしてみます
つぎの ページ で その せいしつを かんがえてみます …
すうがく が すきなひと むけの ないように なっています …
きょうみ あるかたは みてみてください ωについて
---------------------------------------------
→ ≫もどる ≫メニュー ≫ハニーオメガ
こちらの図 クリック↓の▽---------------------------------------------
3時ほうこうが じっすうプラス
9時ほうこうが じっすうマイナス
11時ほうこうが じゅんせいオメガ
2時ほうこうが ハニーオメガー
はんけい2 になっているから
パロロは 2倍で ヒトナミニ(ルート3)でかかれている
はんぶん 0.5 も 2倍でプラスマイナス1でかかれている
はんけい1 の 図よりも でてくるすうじ が すっきりしていて みやすくなっています
----------------------------------------------------------------
2i-omegaる
 ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ≫ もどる ≫ メニュー ≫ しょすう 乗 ≫ きょすう
メモぺーじ
※このページは 数 学 の すきな ひとむき の ないよう になっています
HONEY OMEGA
 (デフォルトせってい …かくにんちゅう) ω =: 0.866ⅰ + 0.5 1 の原始累乗根(いちのげんしるいじょうこん) ハニーオメガー オメガーアンダーバー オメガーシックスーティ ロクジュウドオメガ リトルオメガー ハーフオメガー ルートオメガ ぜったいち |1| ∠ 60 °の ふくそすう  3 じょう すると じっすう マイナス1 に なる 6 じょう すると じっすう プラス 1 に なる |
 |
2 じょう で オメガ ハニーオメガ 2 じょう = オメガ ω 2 = ω |
…★0じょう …★1じょう …★2じょう …★3じょう …★4じょう …★5じょう …★6じょう …  __以下↓の 内容旧定義(12乗根)__ 修正中 (→6乗根へ) |
→ じっすうマイナスいち→ オメガーアイ→ オメガーバー→ マイナスアイ→ マイナスオメガ→ ハニーオメガーバー→ ★ じっすういち
『 なんとか オメガ 』 という なまえ の ついた かしょ は
12 かしょ ちゅう 8 かしょ あり
かならず 50% と 86.6% の セットに なっています …
プラスマイナスつけて ふくそすう っぽくかくと …
なんとか おめが = ±0.5 ( きょ or じつ ) ± 0.866 ( じつ or きょ )
で 8 しゅるい
それに じゅんきょすう が プラスマイナス で 2 しゅるい
さいごに いちばん なじみのある じっすう 1 もプラスマイナスで 2 しゅるい
ごうけい 12 しゅるい の ふくそすう
|
。。。。 。。。。 。。。。 |

| ネーミング きじゅん |
||
 |
プラス | ブレ が 0° の ほうこう (ほんりょうはっき) |
| マイナス | 180 ° くわえる (げんてん たいしょう) | |
| アイ | 90 ° くわえる (すいちょく) | |
| バー | じょうげ たいしょう (きょうやく) | |
| ルート | カクド はんぶん | |
| じじょう | カクド ばい | |
| さんじょう | カクド さんばい | |
| よんじょう | カクド よんばい |
| デフォルトせってい | ||||||
| しすう | ほうこう の 名 | プラス かくど | じゅんきょすう | マイナス1 | べつていぎ | |
| ⓪ | じっすうプラス | ∠ 0° | ⅰ^0 | (-1)^0 | ||
| ① | ハニーオメガ | ∠ 30° | ⅰ^0.333 | (-1)^0.166 | ルートルートオメガ | |
| ② | ルートオメガ | ∠ 60° | ⅰ^0.666 | (-1)^0.333 | マイナスオメガバー | |
| ③ | じゅんきょすうアイ | ∠ 90° | ⅰ^1 | (-1)^0.5 | ||
| ④ | じゅんせいオメガ | ∠ 120° | ⅰ^1.333 | (-1)^0.666 | 4じょうオメガ | ハニーオメガーアイ |
| ⑤ | ルートオメガーアイ | ∠ 150° | ⅰ^1.666 | (-1)^0.833 | マイナスハニーオメガーバー | |
| ⑥ | じっすうマイナス | ∠ 180° | ⅰ^2 | (-1)^1 | ||
| ⑦ | オメガーアイ | ∠ 210° | ⅰ^2.333 | (-1)^1.166 | マイナスハニーオメガ | |
| ⑧ | オメガーバー | ∠ 240° | ⅰ^2.666 | (-1)^1.333 | オメガじじょう | オメガぶんのいち |
| ⑨ | マイナスアイ | ∠ 270° | ⅰ^3 | (-1)^1.5 | ||
| ⑩ | マイナスオメガー | ∠ 300° | ⅰ^3.333 | (-1)^1.666 | ルートオメガーバー | |
| ⑪ | ハニーオメガーバー | ∠ 330° | ⅰ^3.666 | (-1)^1.833 | ハニーオメガのぎゃくすう | |
| ⑫ | じっすうプラス | ∠ 360° | ⅰ^4 | (-1)^2 |
。。。。。。。。。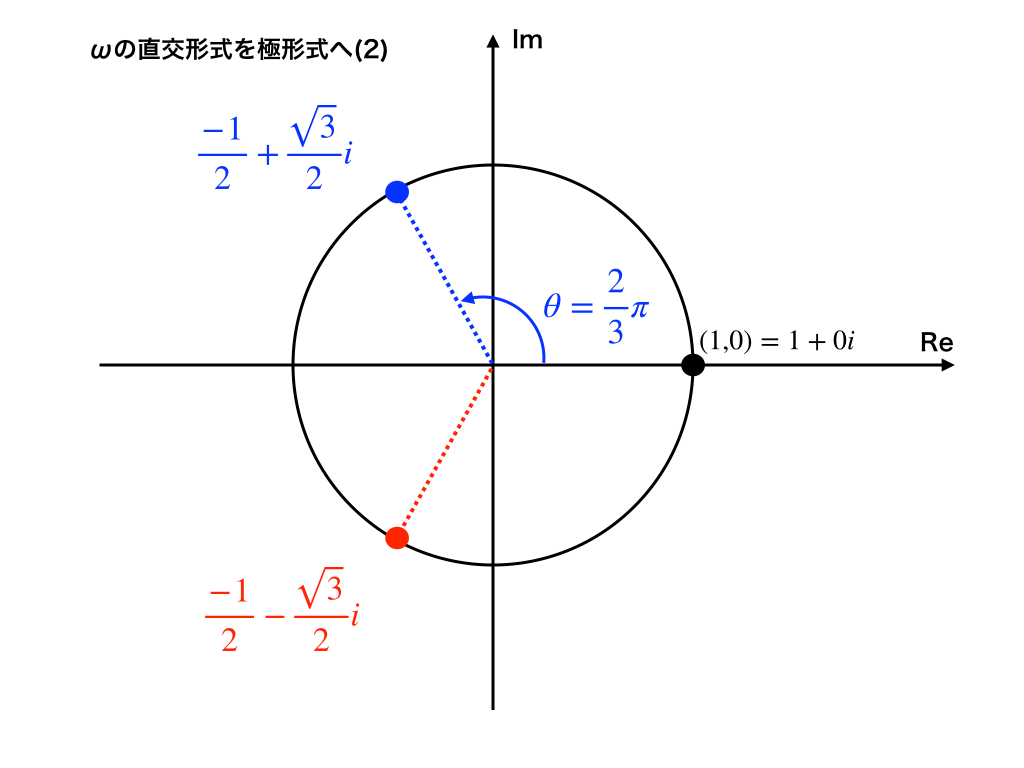 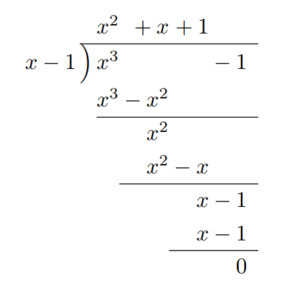 |
たてじく には さいごに きょすう アイ ⅰ が くっついて きます。 この くっついた じょうたい を むずかしい ことばで 複素数 ( ふくそすう ) とかいいます … ( ※ようするに きょじつ こんざい すう。みたいな イメージです ) +0.5 +0.866ⅰ +0.5 -0.866ⅰ -0.5 +0.866ⅰ ←つうしょう オメガ …マイナス れいてんご と パロロアイ …とおぼえてます <(_ _)> -0.5 -0.866ⅰ +0.5ⅰ+0.866 +0.5ⅰ-0.866 -0.5ⅰ+0.866 -0.5ⅰ-0.866 じっすう +1.0 +0.000ⅰ -1.0 +0.000ⅰ じゅんきょすう +1.0ⅰ+0.000 -1.0ⅰ+0.000 つうじょうは 120度 かいてん した -0.5 + 0.866ⅰ という すうじ を オメガ とよぶことにして … -0.5 - 0.866ⅰ という すうじ を オメガーバー とよぶことにする … けいさん を して いく ばあいが おおいです … わたしは -0.5 + 0.866ⅰ ←これ を じゅんせい の オメガ と よぶことにしてみます …<(_ _)> ほんしつてきに ただしくするなら きょぶ の フゴウ は ± が みかくてい で どちら か を きめるまでは … ±きょぶ りょうほう の かのうせい を ひめている すうじ です … じゅんせいオメガにはこれらのせいしつが あるようです … 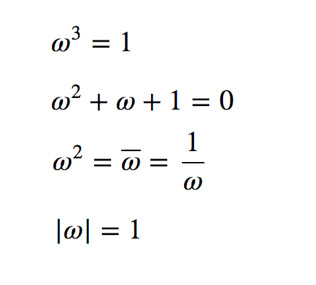 オメガー の もとめかた … ▽-------------- x3 = 1 3 じょう すると 1 になる かず は なんですか ? といういみで … ひとつ は 1 で。 あと 2つ の オメガー が いるようで。 これ を 『 かい の こうしき 』 で とくと ★ じゅんせい オメガー や ★ オメガーバー が でてきます … ユーチューブ でまなばさせてもらいました …→ (きょうやくのよびかたがぎゃくてんするばあいもよくあるようです) |
| デフォルトせってい | ||||||
| しすう | ほうこう の 名 | プラス かくど | じゅんきょすう | マイナス1 | べつていぎ | (カッコ)は ねん のため |
| ⓪ | じっすうプラス | ∠ 0° | ⅰ^0 | (-1)^0 | +1 | |
| ① | ハニーオメガ | ∠ 30° | ⅰ^0.333 | (-1)^0.166 | ルートルートオメガ | ω |
| ② | ルートオメガ | ∠ 60° | ⅰ^0.666 | (-1)^0.333 | マイナスオメガバー | (√ω) |
| ③ | じゅんきょすうアイ | ∠ 90° | ⅰ^1 | (-1)^0.5 | ⅰ | |
| ④ | じゅんせいオメガ | ∠ 120° | ⅰ^1.333 | (-1)^0.666 | 4じょうオメガ | ω |
| ⑤ | ルートオメガーアイ | ∠ 150° | ⅰ^1.666 | (-1)^0.833 | マイナスハニーオメガーバー | (ⅰ√ω) |
| ⑥ | じっすうマイナス | ∠ 180° | ⅰ^2 | (-1)^1 | -1 | |
| ⑦ | オメガーアイ | ∠ 210° | ⅰ^2.333 | (-1)^1.166 | マイナスハニーオメガ | (ωⅰ) |
| ⑧ | オメガーバー | ∠ 240° | ⅰ^2.666 | (-1)^1.333 | オメガじじょう | ω |
| ⑨ | マイナスアイ | ∠ 270° | ⅰ^3 | (-1)^1.5 | -ⅰ | |
| ⑩ | マイナスオメガー | ∠ 300° | ⅰ^3.333 | (-1)^1.666 | ルートオメガーバー | (-ω) |
| ⑪ | ハニーオメガーバー | ∠ 330° | ⅰ^3.666 | (-1)^1.833 | ハニーオメガのぎゃくすう | ω |
| ⑫ | じっすうプラス | ∠ 360° | ⅰ^4 | (-1)^2 | +1 |
| 。。。。。。 | ω =: 0.5ⅰ+ 0.866 よく みると ひとつ まえに みた しき と ならび が かわっただけです … こいつ を じじょう … さんじょう … よんじょう …と つづけていくと … 30度ずつ かいてん していき … ページトップ に あった 12 せいざ マーク の 地点 を じゅんに まわっていきます … 12 じょう ( 12 回 ) めで ぴったり もとの プラス1 ( ゼロ度 かいてん ) に もどってきます … クリックすると そのけいさん が かくにん できる サイト へ ジャンプ します … 1じょう …2じょう …3じょう …4じょう …5じょう …6じょう … 7じょう …8じょう …9じょう …10じょう …11じょう …12じょう … Q; 11 じょう も 12 じょう も したら … もとに もどって くる どころか … 5 × 5 × 5 = 125 …3 じょう だけでも ケタ ちがい …のように … めちゃくちゃ すうじ が おおきく なってしまうのでは …? …と、もしかしたら 、ちょっかんが はたらく かも しれません … A; しかし、だいじょうぶ です。 12 じょう で もとに しっかり もどってきます … なぜなら … オメガ は いち や マイナス1 …きょすうアイ …の なかまで … |ぜったいち|が 1 の かず だからです。 ω = |1| ぜったいち とは げんてん から の キョリ。になります … 1 は なんじょう しても …1です … 1 × 1 × 1 × 1 × 1 × 1 …= 1 ひゃく じょうしても … しょうすうじょうしても …マイナスじょうしても … = 1 です つまり オメガ も ハンケイ 1 の げんてん キョリ を ぐるぐる まわる だけで … けいすう が ひっついて ( さらに けいすうごと かっこ でくくられてい) ないかぎり … ぜったいち が おおきく なっていくことは ないです …
|
 |
|
4 じょう で オメガ ハニーオメガ^4 = じゅんせい オメガ ω 4 = ω |
3 じょう で アイ ハニーオメガ^3 = じゅんきょすう アイ ω 3 = ⅰ |
ハニーオメガーは じゅんせいオメガ や じゅんきょすうアイ への へんかん に すぐれています … ( しょうすうじょう や ぶんすうじょう を つかうことなく しぜんすうじょう ( ルイ乗 ) で へんかん できます …) |
|
じっすう マイナス1 や じっすうプラス1 にも なります
12じょう で じっすうプラス1。
ハニーオメガ^12 = じっすうプラス1
ω^12 = 1
6じょう で じっすうマイナス1。
ハニーオメガ^6 = じっすうマイナス1
ω^6 = -1
12じょう で プラス1になるということは …
いままでの すべての じっすう けいさん の うしろに
ハニーオメガ12じょうを ひっつけても なんら かわらない …
ということをイミすることになります …(←かくにんちゅう)
たとえるなら …
| しょうすう …てんゼロ。ということば を せいすう の うしろに ひっつけても … なんら いみ は かわらない … 2=2.0 3=3.0 100=100.0 |
。。。。 | ぶんすう いちぶんの…。ということば を せいすう の うしろに ひっつけても … なんら いみ は かわらない … 2 3 100 2=― 3=― 100=―― 1 1 1 |
どういうイミかというと …
ω^12 = 1
すべて の かずの うしろには
【×1】 が しょうりゃくされている といるとかんがえてみます …
2=2×1 3=3×1 4=4×1 100=100×1 0.05=0.05×1 -2=-2×1
2+3=2×1+3×1 ( =5 )
【1( いち )】 というのは 【 ハニーオメガーの じゅうにじょう 】 でした …
つまり
2=2×1
=2×ω^12
=2ω^12
3.3=3.3×1
=3.3×ω^12
=3.3ω^12
100=100×1
=100×ω^12
=100ω^12
-67=-67×1
=-67×ω^12
=-67ω^12 (=67ω^6も)
2
≫![]()
3i-omegaる
 ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ≫ もどる ≫ メニュー ≫ しょすう 乗 ≫ きょすう
みかくにん
ちょうせいちゅう
シミュレーション メモ
| ω | = |  |
= +0.5i + 0.866 |
| ω×ω | = |  |
= +0.5i + 0.866i |
| ω×ω×ω | = |  |
= +ⅰ |
| ω×ω×ω×ω | = |  |
= -0.5i + 0.866i |
| ω×ω×ω×ω×ω | = |  |
= +0.5i - 0.866 |
| ω×ω×ω×ω×ω×ω | = |  |
= -1 |
| (ページはば で ^7 じょうに へんこうします→) ω7 | = |  |
= -0.5i - 0.866 |
| ω×ω7 | = |  |
= -0.5i - 0.866i |
| ω×ω×ω7 | = |  |
= -ⅰ |
| ω×ω×ω×ω7 | = |  |
= +0.5i - 0.866i |
| ω×ω×ω×ω×ω7 | = |  |
= -0.5i + 0.866 |
| ω×ω×ω×ω×ω×ω7 | = |  |
= +1 |
| ω×ω×ω×ω×ω×ω0 | = | ω12 | = +1 |
| ω×ω×ω×ω0+ω0 | = 1 + 1 = 2 | ||
たしざん ひきざん
| じぶん | たす | じぶん | は に | こぶん | じぶん | ひく | じぶん | は ゼロ | (原点オー) |
||
 |
+ |  |
= 2 |  |
。。。。。。。  。。。。。。 。。。。。。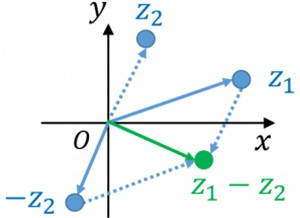 たしざん は へいこうしへんけい で ごうりゅうする   |
 |
ー |  |
= 0 | ||
 |
+ |  |
= 2 |  |
 |
ー |  |
= 0 | |||
 |
+ |  |
= 2 |  |
 |
ー |  |
= 0 | |||
 |
+ |  |
= 2 |  |
 |
ー |  |
= 0 | |||
 |
+ |  |
= 2 |  |
 |
ー |  |
= 0 | |||
 |
+ |  |
= 2 |  |
 |
ー |  |
= 0 | |||
 |
+ |  |
= 2 |  |
 |
ー |  |
= 0 | |||
 |
+ |  |
= 2 |  |
 |
ー |  |
= 0 | |||
 |
+ |  |
= 2 |  |
 |
ー |  |
= 0 | |||
 |
+ |  |
= 2 |  |
 |
ー |  |
= 0 | |||
 |
+ |  |
= 2 |  |
 |
ー |  |
= 0 | |||
 |
+ |  |
= 2 |  |
 |
ー |  |
= 0 | |||
| けいすう が ないとき カケザン は オメガ^(しすう)のたしざん になる ωA × ωB = ω(A+B) |
けいすう が ないとき ワリザン は オメガ^(しすう)のひきざん になる ωA ÷ ωB = ω(A-B) |
||||||||||
 |
× |  |
= |  |
 |
÷ |  |
= |  |
||
 |
× |  |
= |  |
 |
÷ |  |
= |  |
||
 |
× |  |
= |  |
 |
÷ |  |
= |  |
||
 |
× |  |
= |  |
 |
÷ |  |
= |  |
||
 |
× |  |
= |  |
 |
÷ |  |
= |  |
||
 |
× |  |
= |  |
 |
÷ |  |
= |  |
||
| 類似色 表現 要確認 |
中間色 | パロロ 86.6% 2回ぶん (ヒトナミニ) |
ハニーオメガ+6(はんたいしょく) は あいうちになる |
||||||||
 |
+ |  |
=1.73 |  |
 |
+ |  |
= 0 | |||
 |
+ |  |
=1.73 |  |
 |
+ |  |
= 0 | |||
 |
+ |  |
=1.73 |  |
 |
+ |  |
= 0 | |||
 |
+ |  |
=1.73 |  |
 |
+ |  |
= 0 | |||
 |
+ |  |
=1.73 |  |
 |
+ |  |
= 0 | |||
 |
+ |  |
=1.73 |  |
 |
+ |  |
= 0 | |||
120度 かんけい なら 1こぶん の 60度 |
|||||||||||
 |
+ |  |
= |  |
|||||||
 |
+ |  |
= |  |
|||||||
 |
+ |  |
= |  |
|||||||
 |
+ |  |
= |  |
|||||||
 |
+ |  |
= |  |
|||||||
 |
+ |  |
= |  |
|||||||
4i-omegaる
 ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ̄ ≫ もどる ≫ メニュー ≫ しょすう 乗 ≫ きょすう
width=1366 →1336
≫もどる ≫メニュー ≫オメガ と パロロ ≫ハニーオメガー ≫きょすう
※メモファイル
【 よい 】 という コトバ が いちじげん では …
なにか が なにか を しはい する こうぞう は さけられません …
だい は しょう を かねる
かんじ どりる 1・ 2
その ひと に とって の プラス の ほうこう =: 【 よ さ 】
と ていぎ してみて …
もし その 【 よ さ 】 という かちかん が
ふくそすう のように
はなせる コトバ として そんざい した なら …
その ひと ほんにんに とっても …
その まわり の ひとに とっても …
あっとうてき に
おたがい の かちかん を
みとめあいやすい しゃかい に なる ハズ です
たとえば
(和風月名)
(干支)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
いちりつ わたくしりつ
かがく ばけがく
≫オメガ と パロロ
.png)
ようするに
ド・ストライク ( ブレ ∠0 度 ) は …
100 パーセント
( そのまま の とうしんだいで につたわる )
ダイレクト
1こ となり ( ブレ ∠30 度 ) は …
87パーセント
( だいたい 13% ほどは わるぎなく!! けづれた じょうたいで つたわる )
(でんごんゲームおもいだしてください)
2こ となり ( ブレ ∠60 度 ) は …
はんがく
( ちょうど はんぶん わるぎなく!! けづれた じょうたいで つたわる )
の えいきょう ってこと が いいたい わけです
その せいしつ は どの ほうこうに むいている いしき に とっても
みんな びょうどう!!
ってことです …
.jpg)
【 ※ ない (ゼロ な) 】 のでは ない
いち(=1) という おおきさを …
【 ※ ひめている 】
たとえば …
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
↑
つぎ の ひょう は たんじゅん に やじるし の むき が
(←→) ぎゃく に なった だけです …
↓
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
【 よい 】 という ことば が いちじげん では …
なにか が なにか を しはい する こうぞう は さけられません …
かんじ どりる 1・ 2
そのひとにとっての プラス ほうこう =: 【 よ さ 】
【 よ さ 】 は ふくそすう の かいてん
ひと(← の かちかん)
そこにたてまえの りょういき を できるかぎり ちいさく したい …
たてまえ は きょすういみ になるので …
それを いれると …
このことばの そんざいいみ が じょじょに なくなっていきます
きょうちょうせいのたかいひとほど …
そこは (※ほんとうの) ほんね で あることが もとめられます …
よさ わるさ という ことばに ごまかし の りょういき を
できるだけ ちいさく していく かちかん の ことば …
 ̄ ̄ ̄ ̄ ̄ ̄ ̄
ひと ( ← の かちかん)
そこに どうしても いれてしまう 【 たてまえ 】 の りょういき …
それを できるかぎり ちいさく したい …
【 たてまえ 】 は きょすう いみ になるので …
...................bubuzuke........
ⅰ ≠ 0
それ を 【 よい 】 もの だと しゅうかんかさせて しまうと …
ⅰ ≠ 1
たんきてき ・ ちょくせつてき な ひずみ は さけられたとしても …
それ は なくなった のではなく
もちこされた …だけであり …
その しわよせは たちば の よわいもの へと
ふくらんだじょうたいで うけつがれていきます …
そのけっか …
【 よい 】 …という コトバ の いみ さえも じょじょに うすめていきます …
よさ ・ わるさ という ことば に おける
あいまい な ひびきの りょういき を
できるだけ ちいさく していく かちかん の コトバ …
 。。
。。




 。。
。。

 。。
。。 。。
。。

 。。
。。



 。。
。。

 。。
。。 。。
。。
