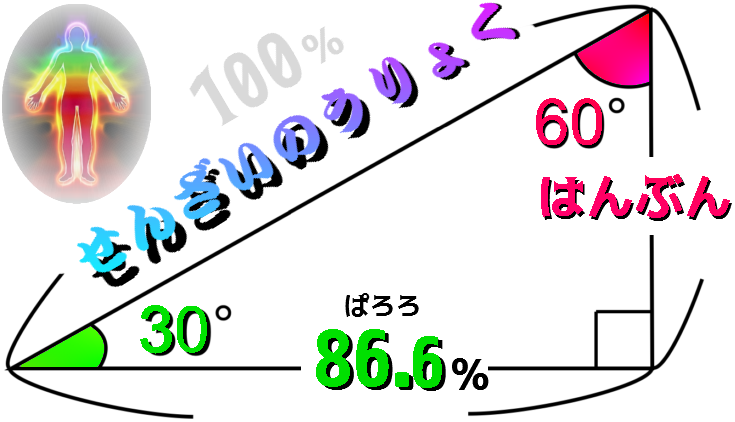
240211 むつき きさらぎ ねうしとら よい すうじあん おたがいにとって 50 % ( 86.6 %)
もどる
きーわーど 『 な る ほ ど 』

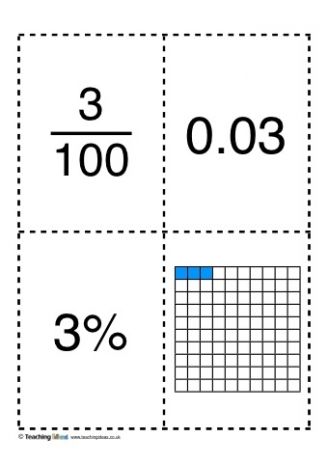
はっき される イメージ こうか として あらわれてくる わりあい
しごとりつ えいきょう を あたえる ひりつ はたらいてくる むくわれてくる %
.jpeg)
.png)
 inrou -mito
inrou -mitoきーわーど 『 な ○ ○ ○ 』
.png)
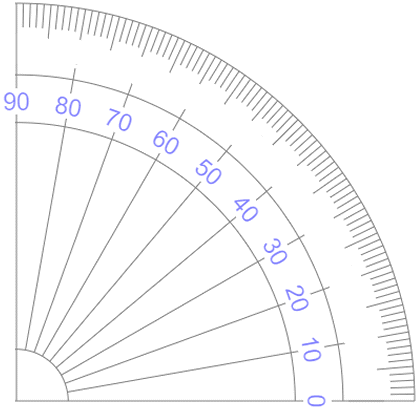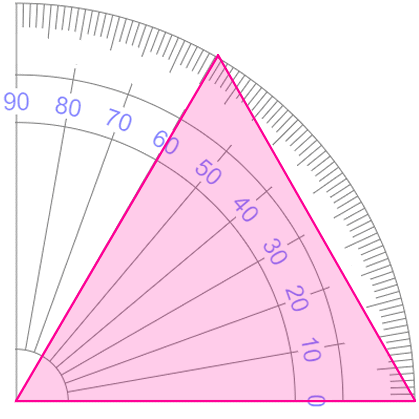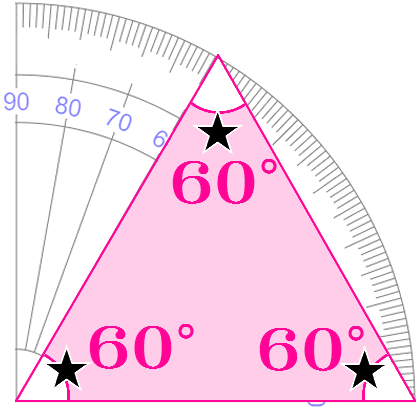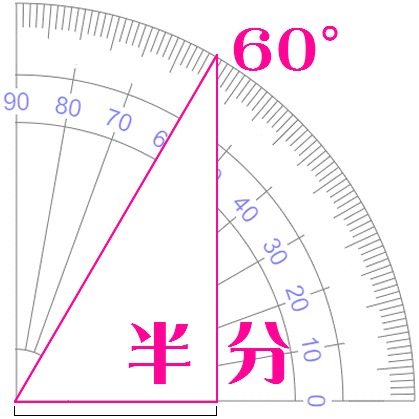
青果コーナー リンゴ ゾウ
≫ もどる ≫ マップ ① ② ③ ④ ⑤ ≫ あーぎゅめんと ≫ しす カケザン ≫ ..ビジョン ≫ 2アイ2 ..≫ 100 ≫ 4 じょう
240211 むつき きさらぎ ねうしとら よい すうじあん おたがいにとって 50 % ( 86.6 %)
もどる
きーわーど 『 な る ほ ど 』





はっき される イメージ こうか として あらわれてくる わりあい
しごとりつ えいきょう を あたえる ひりつ はたらいてくる むくわれてくる %


.jpeg)
.png)

 inrou -mito
inrou -mito
きーわーど 『 な ○ ○ ○ 』
.png)




青果コーナー リンゴ ゾウ
   カエル 60°はんぶん .jpg) .jpg) .jpg) .jpg) .jpg)    きーわーど 『 な ○ ○ ○ 』 |
リンゴ が すきな ランボー くん .jpg) 3 × 2 = 6 2 × 5 = 10 1 × 7 = 7 6 × 6 = 36 しす の かたち に かえます 3 ( 0ど ) × 2 ( 0ど ) = 6 ( 0ど ) 2 ( 0ど ) × 5 ( 0ど ) = 10 ( 0ど ) 1 ( 0ど ) × 7 ( 0ど ) = 7 ( 0ど ) 6 ( 0ど ) × 6 ( 0ど ) = 36 ( 0ど ) きーわーど 『 な ○ ○ ○ 』 おたがい に とって 50 % ( 86.6 % ) プラチナ 比 ルート 3 ひとなみに 1.7320508 1.73 歩 まえ に すすんで よこに カニ あるき 1 歩 で もとの いち から 30 ど ずれ ぱろろ ひとなみ の はんぶん ( √0.75) ( cos30°) なぜ 、 『 おたがいに とって 』 … といえるのか? ① 1.73 歩 すすむ 話 この話 は どっちの 方 向 ( 東西南北 ) に むいている ひと にとっても おなじように いえる ことだから … ② 3じょう わる 2じょう の 話 33 × 32 = 3○ 27 ÷ 9 = 3 33 ÷ 32 = 3 ( 3 × 3 × 3 ) ÷ ( 3 × 3 ) これは 3 に かぎらず、 すべての かず (.. 2 ・ 4 ・ 5 ...10 ...) で つかえる 1000 ÷ 100 = 10 きょすう オメガ でも、 ω3 ÷ ω2 = ω ( 6 じょうこん ていぎ ハニーオメガ でも、) ω3 ÷ ω2 = ω りゆう は シンプル 『 かけざん の ぎゃく えんざん が わりざん だから … 』 1ど かけた すうじ を もとに もどしたかったら おなじすうじ で われば もとに もどるから … おおくの かちかん が そんちょう されやすく なるのか? ぎゃく に すべてに たいして プラス の ほうこう の かのうせい を こうりょ する なら、 はなし が 1歩 も まえに すすまなくなる のでは? ぜったいち 1 では 、 どれだけ こうりょ ( ×÷ ) しても まえ には すすみません … そこで ぜったいち と カクド りょうほう が こうりょ されれば まえに すすめることが できます … .jpg) |
りんご 画像 けんさく
あーぎゅめんと excel
ふくそすう を かくど で しめします
しす の 逆引き excel
ふくそすう を しす の かたち に かえます