2401117 えくせる おたがいにとって 50 %
≫ もどる ≫ マップ 2D さんこう 動 画 1yyi2ak3twi 先 週 ≫ ピタゴラス+02 「 ぴったり 」 じゃない としても 10 °おき 2309
2401117 えくせる おたがいにとって 50 % ![]()
![]() ...
... ![]() 7 ふくろ の ほうが わけやすい? 8カンスウ ゴロセット
7 ふくろ の ほうが わけやすい? 8カンスウ ゴロセット




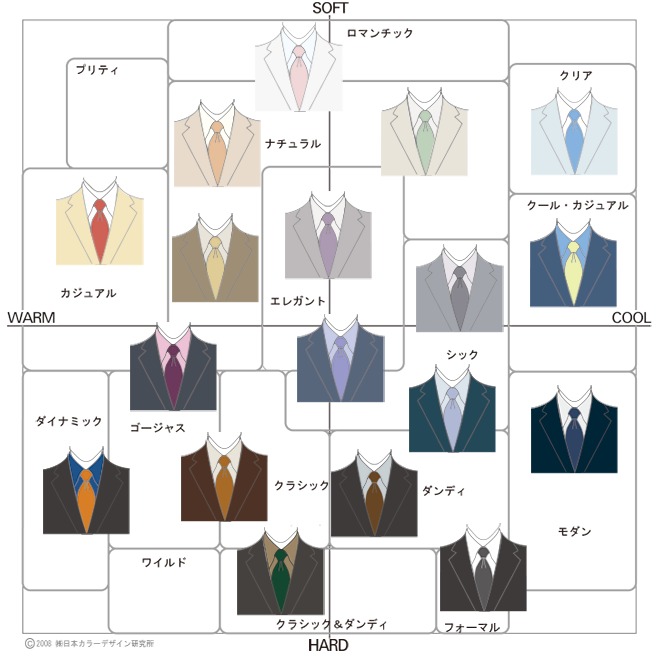


 映6 7 8 9算10グ11鯛12二13分14
映6 7 8 9算10グ11鯛12二13分14
きーわーど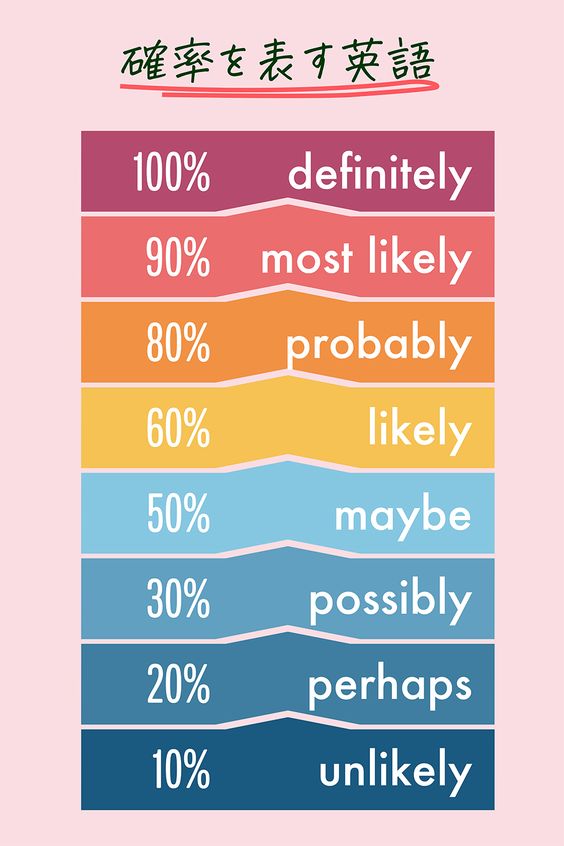 |
『 な る ほ ど 』 『 ようするに 』 『 ひめている 』 |
『 ろっかくよい 』 |
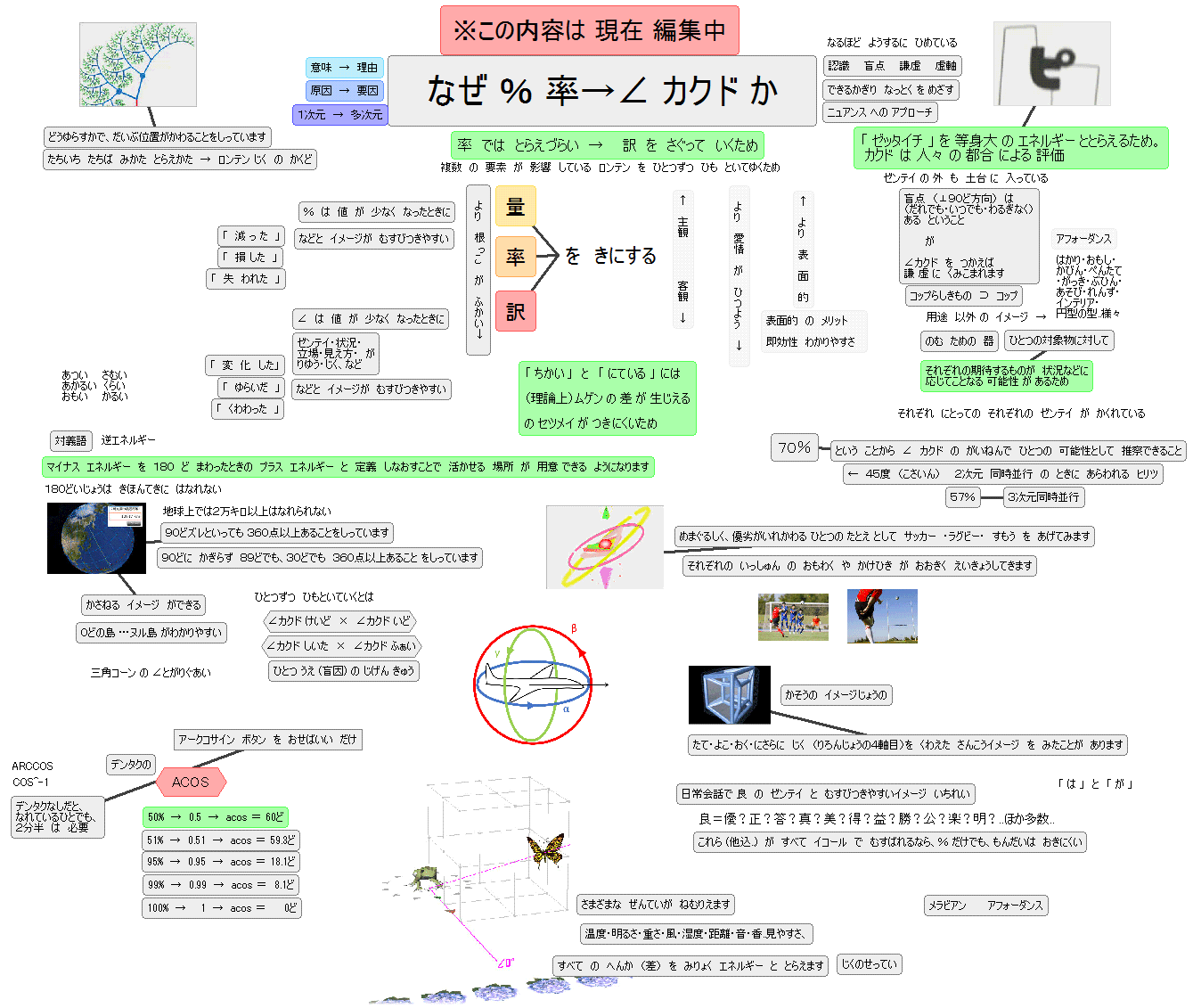
意味 → 理由 原因 → 要因 1次元 → 多次元 |
 |
認識 盲点 謙虚 虚軸 できるかぎり なっとく を めざす ニュアンス への アプローチ |
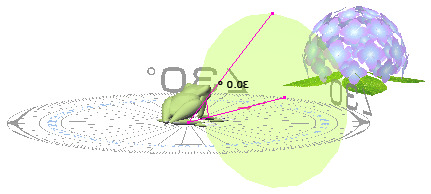


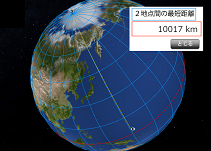 1 2
1 2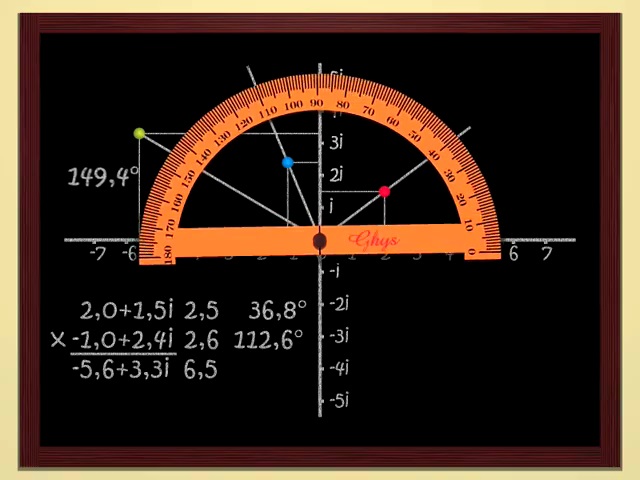

.jpg)
.jpg)
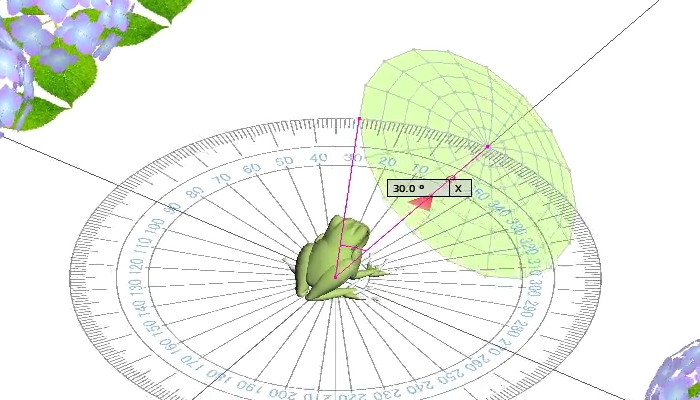

.jpeg)


.jpg)
.jpg)
 【 よ い 】
【 よ い 】 .jpeg)
.jpg)
.jpg)
.jpeg)

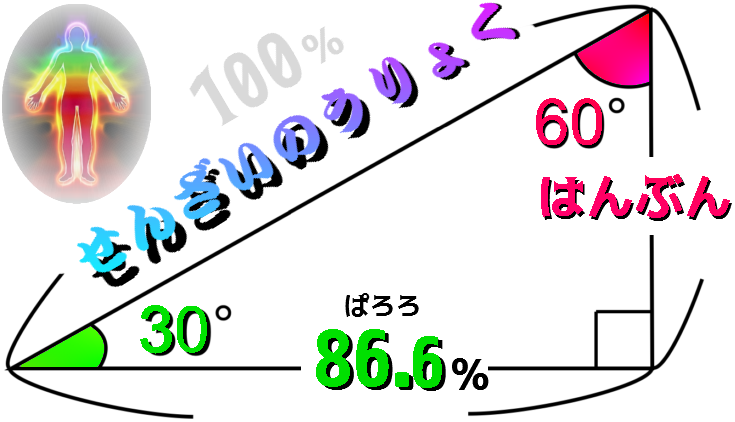
さんこう 動 画 よんへいほう
もどる
ピタゴラス
【重要】18 次元ピタゴラス
(1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 1, 2, 4, 6) (1,1,1,1,1,1,1,1,1,1,1,2,2,3,3,
3, 3, 3, 8) (1,1,1,1,1,1,1,1,1,1,1,1,2,2,2, 4, 4, 5, 9)
(1,1,1,1,1,1,1,1,1,1,1,1,2,2,2, 2, 2, 2, 6) (1,1,1,1,1,1,1,1,1,1,1,1,1,2,2, 3, 3, 5, 8) (1,1,1,1,1,1,1,1,1,1,1,1,2,2,2, 2, 2, 7, 9)
(1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 3, 3, 4, 7) (1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,
2, 3, 6, 8) (1,1,1,1,1,1,1,1,1,1,1,1,1,1,1, 4, 5, 5, 9)
【重要】6次元ピタゴラス
(1,1,1,1,1, 2, 3) (1,1,1,1,6, 9, 11) (1,1,1,2,5, 7, 9) (1,1,1,3,4,
6, 8)
(1,1,1,1,3, 6, 7) (1,1,1,2,2, 5, 6) (1,1,1,2,9, 9, 13) (1,1,1,4,5,
10, 12)
(1,1,1,1,4, 4, 6) (1,1,1,2,3, 3, 5) (1,1,1,3,3, 10, 11) (1,1,1,5,6,
6, 10)
【重要】5次元ピタゴラス
(1,1,1,2,3, 4) (1,1,2,3,7, 8) (1,1,5,6,9, 12) (2,2,2,3,10, 11)
(1,1,1,4,9, 10) (1,1,3,3,4, 6) (1,1,7,8,9, 14) (2,2,3,4, 4, 7)
(1,1,1,5,6, 8) (1,1,3,5,8, 10) (2,2,2,2,3, 5) (2,2,4,4, 9, 11)
【重要】4次元ピタゴラス数.txt txtフォルダ
4 + 16 + 36 + 169 = 225 (2,4,6,13,15)
(1,1, 1, 1, 2) (1,1, 3, 5, 6) (1,1, 5,13,14) (1,1, 7, 7,10)
(1,1,11,19,22) (1,2, 2, 4, 5) (1,2, 4,10,11) (1,2, 6,20,21)
(1,2, 8,10,13) (1,2,10,16,19) (1,2,18,20,27) (2,4, 6,13,15)
【重要】3次元ピタゴラス
(1, 4, 8, 9) (2, 2, 1, 3) (2, 6, 9,11) (2, 4, 4,a 6)
(2, 3, 6, 7) (2, 5,14,15) (2, 7,26,27) (2, 8,16,a18)
(2, 9,42,43) (2,10,25,27) (6,10,33,35) (6,14,57,59)
2D↓ ( ふつうのピタゴラス ) ↓
【重要】2次元ピタゴラス
( 3, 4, 5) ( 5, 12, 13) ( 8, 15, 17) ( 7, 24, 25)
(20, 21, 29) (12, 35,37) ( 9, 40, 41) (28, 45, 53)
(11, 60, 61) (16, 63, 65) (33, 56, 65) (48, 55, 73)
【重要】1次元ピタゴラス
(1, 1) ( 2, 2) ( 3, 3) ( 4, 4)
(5, 5) ( 6, 6) ( 7, 7) ( 8, 8)
(9, 9) (10,10) (11,11) (12,12)
タテ 6 : ヨコ 8
ろっかくよい jibun-you memo mienai file idou shita 240725 folder idou file
もどる